이번주 위클리 페이퍼의 주제는
HashSet의 내부 동작 방식과 중복 제거 메커니즘을 설명하고, HashSet이 효율적인 중복 체크를 할 수 있는 이유를 설명해보자
O(n)과 O(log n)의 성능 차이를 실생활 예시를 들어 설명하고, 데이터의 크기가 1백만 개일 때 각각 대략 몇 번의 연산이 필요한지 비교해보자
해시 함수는 어떤 입력값을 받아서, 고정된 크기의 해시값(숫자)으로 변환해주는 함수이다.
같은 입력값은 항상 같은 해시값으로 계산된다. HashMap, HashSet 등 자료구조에서 사용된다.
이 중 HashSet에 대해 알아볼 것이다. HashSet은 내부적으로는 HashMap을 기반으로 동작한다.
HashSet 해시 테이블을 이용하여 데이터를 저장하는 구조이다. 중복 값이 저장되지 않는 Set의 특징을 가지고 있다.
HashSet의 내부 동작 방식
HashSet은 내부적으로는 HashMap을 기반으로 동작한다. 즉 HashSet은 입력값을 HashMap의 Key에 저장한다.
HashSet에 객체를 추가하면 내부적으로 hashCode() 메서드를 호출하여 해시값을 구한다.
그다음 equals() 메서드를 호출한다.
equals() 메서드로 계산한 해시 값의에 이미 동일한 객체가 있는지 확인한다.
따라서 HashSet은 중복 제거 매커니즘으로 hashCode()와 equals()를 사용한다.
그렇다면 왜 HashSet이 효율적으로 중복 체크를 할 수 있는 걸까? 대부분의 경우 hash 값만으로도 위치를 빠르게 찾을 수 있고 해시충돌 시에도 equals() 연산으로 비교만 하면 되기 때문에 연산량도 적다.
O(n)과 O(log n)
O(n)과 O(log n)은 주로 시간복잡도를 나타낼 때 사용한다.
시간복잡도란 알고리즘이 처리해야 할 데이터 양(n)이 증가할 때, 실행 시간(또는 연산 횟수)이 얼마나 증가하는지를 수학적으로 표현한 것이다.
그 중에서 Big-O 표기법은 최악의 경우를 상정한 실행 시간을 나타낸다.
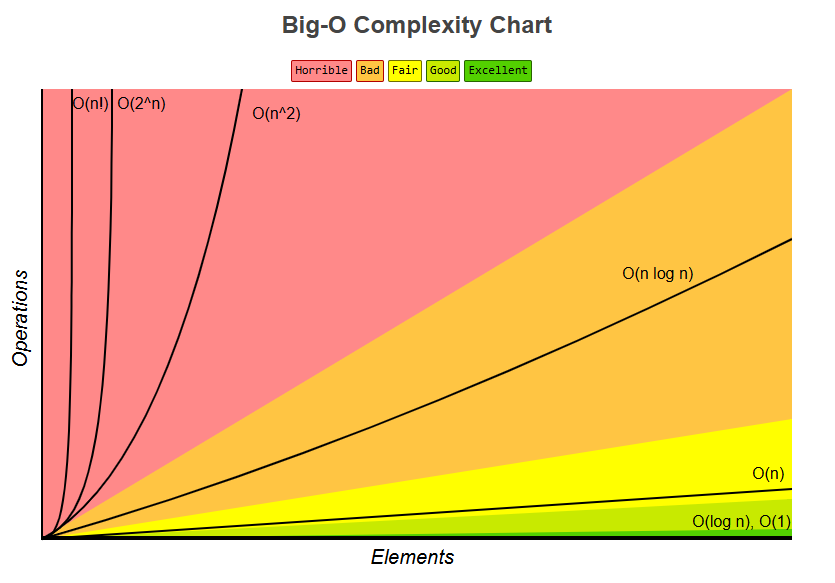
[출처]: https://www.bigocheatsheet.com/
위표에서 볼 수 있듯이 O(n)과 O(log n)은 괜찮은 증가율을 가지고 있다.
O(n)은 말그대로 처리할 데이터 양인 n이 증가할 수록 같은 비율로 처리 시간이 증가하는 복잡도이다.
코드에서 for문을 하나 사용할 시 O(n)의 복잡도를 가진다.
따라서 입력값의 크기가 1백만 개라면 O(n)의 알고리즘은 최대 1백만번 연산을 해야한다.
O(log n)은 입력값 n이 증가할 수록 처리 시간이 log 만큼 줄어든다.
대표적인 예시로 이진탐색트리(Binary Search Tree, BST)가 있다.
log₂(n)에서 입력값 n이 1000개 일 때 연산 횟수는 약 10번 이고, 입력값 n이 10배 증가한 10000개라면 연산 횟수는 약 13.3회이다. 입력값이 1000배 증가한 1백만 개여도 연산량은 약 20회로 소량 증가한다!
위와 같이 O(log n)는 입력값이 증가해도 처리 시간이 조금 증가하므로 효율적인 알고리즘이다.
실생활의 예시로 O(n)은 도서관에서 도서 라벨이 붙어있지 않은 책장에서 내가 원하는 책을 찾는 경우가 된다.
최악의 경우 책장에 있는 모든 책을 확인해야 하기 때문에 책이 100권이면 최대 100번, 1000권이면 최대 1000번 확인해야 원하는 결과를 얻을 수 있다.
O(log n)은 사전에서 내가 원하는 단어가 있는 페이지를 찾는 경우이다. 내가 원하는 단어가 korea라면 우선 사전의 가운데 페이지를 펼친 뒤 그곳에 있는 단어보다 내가 찾는 단어가 앞에 있는지 뒤에 있는지 확인한다. 사전의 정중앙 페이지에 M으로 시작하는 단어들이 있다면 K는 그보다 앞에 있으므로 사전 앞쪽의 절반부분을 확인한다. 이번엔 책의 1/2부분에서 다시 정중앙을 펼치고 내가 찾는 단어 초성의 앞뒤 여부를 찾는다.
이런식으로 진행한다면 사전의 페이지가 1000장이라면 약 10번만 탐색해도 원하는 페이지를 찾을 수 있을 것이다.
'Weekly Paper' 카테고리의 다른 글
| [위클리 페이퍼] AOP, @Controller와 @RestController (0) | 2025.05.19 |
|---|---|
| [위클리 페이퍼] 웹서버와 WAS의 차이, Spring Boot의 Bean 등록 방법 (0) | 2025.05.06 |
| [위클리 페이퍼] 스프링 프레임워크와 일반 자바 라이브러리 (0) | 2025.04.27 |
| [위클리 페이퍼] Java 고급 과정 / SRP, OCP, .map(), .flatMap() (1) | 2025.04.12 |
| [위클리 페이퍼] git 활용 (0) | 2025.04.04 |